The Virtual Tumour, part I

Written by David Orrell. 

 

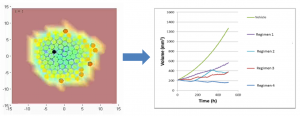
The Virtual Tumour (“VT”) is the main program we use at Physiomics to optimise oncology treatments and predict the effects of drug combinations. This post is the first in a series that will describe the aims, motivations, and some of the history of the project – and gives a peek at the mathematics inside. Today’s topic: why we built the model.

The VT, which in 2019 is now into its tenth year, grew out of a long process where the model adapted and evolved (sort of like tumours actually, but the benign kind) before reaching a relatively stable state. In mathematical modelling, the usual approach is to start with a simple model, and work your way towards something more complicated. With the VT the process has been less straightforward.

When I joined Physiomics in 2007 we were simulating the effects of drugs on cancer cells by using a rather sophisticated model of the cell cycle embedded into a cell population software called SystemCell. This had been developed by a team led by the highly-experienced Oxford Brookes biochemist David Fell who helped start the company and served as Chief Scientific Officer. The model had around a hundred ordinary differential equations (ODEs), and as many parameters.

My background was in mathematical modelling and prediction, and I was coming from the Institute of Systems Biology in Seattle, where I had worked on stochastic models of biological systems. One of my first tasks at Physiomics was to find a way to incorporate stochastic effects due to mitosis into the model. This was part of a project with a large pharma (who will remain anonymous), who wanted us to predict the effects of combination treatments on growing tumours, and optimise the schedule.

As our brochure at the time said, SystemCell could be used to “Support patent applications, Support go/no-go decisions, Illustrate mechanism of action, Rank compounds according to efficacy, Support choice of optimal dosing regimens.” The model had successfully been used in a number of projects for different pharma and biotech companies. However it had a limitation, which was that it was really only designed to simulate a single cell. Yes, we could model a number of such cells, and reproduce things like flow cytometry experiments – but this didn’t account for how cells interact in a growing tumour. And this is what our large pharma company was interested in.

For example, we knew that drug treatment could arrest tumour growth, and then some weeks or months later growth would resume – was this due to something happening at the level of the cell, or was it a population effect, where a small number of cancer cells survive treatment and slowly build in number?

Another phenomenon is what might be called the order effect, where the efficacy of a drug combination depends on the order in which the drugs are taken. For example, taking drug A then drug B might be much less effective than when the order is reversed. We knew that such combination effects could easily boost or diminish the efficacy of a treatment by 50% – which meant that tuning the treatment design could potentially be more worthwhile than tuning the design of the drug itself. Was this due to biochemical effects inside the cell, or was it to do with tumour dynamics?

Our project involved both these effects, so we needed to develop a model which accounted, not just for the cellular dynamics, but for the dynamics and structure of the growing tumour. For example, cells grow and divide and create new cells. They interact with their environment. And as the tumour as a whole increases in size, cells further from the periphery don’t have access to nutrients such as oxygen so tend to become quiescent or necrotic.

Trained mathematical modellers that we were, we were happy to take on this challenge. The logical approach was to use a version of an agent-based model. Each agent represented a cell (actually a representative for a cluster of cells) and would grow and divide to form new cells. The motion of cells as they jostled around was simulated using a force-based algorithm. The nutrient gradient was modelled using partial differential equations. And inside each cell/agent was its own copy of the cell cycle model, running a mix of ODE and stochastic equations, with randomly perturbed parameters that captured the heterogenous nature of the population. Drug concentrations in the plasma were modelled using a coupled pharmacokinetic model.

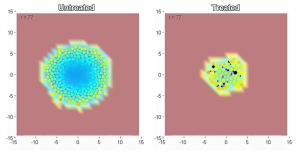
The resulting composite model was magnificently complicated and was used to make rather impressive and convincing videos of tumours that start from a few cells, expand in size with time, develop a necrotic core, and then shrink when exposed to drug. The problem was that we weren’t in the video business – we were trying to predict the effect of anti-cancer drugs. Our predictions were going to be blind-tested against a series of experimental results by a very serious company. And the model, in our eyes, had a major drawback, which was what made it good for videos, made it bad for prediction.

Click here to see the video

These two aspects of models – the descriptive and predictive – are often confused. For example I have been to forecasting conferences where speakers show incredibly realistic model-based simulations of the Earth’s atmosphere, complete with evolving clouds and swirling storm systems, with the unspoken implication that those same models must be very good at predicting the long-term weather (they’re not). Or amazing video simulations of the human heart pumping away, even if the underlying models can’t do better at predicting the effects of a drug than the simplest estimate.

The cell cycle model was perfect for analysis at the level of reactions within the cell, which is what it was designed for, but strapping copies of it into a larger model had multiplied the level of complexity. And a general, if rather counter-intuitive, principle in mathematical modelling is that complicated models are usually not very good at prediction.

In our next post in this series, we look at why this is true – and how we addressed the problem using the Virtual Tumour.